Chapter 8 Additional character types
So far we have considered a single type of character data – DNA sequences. But there are many other types of characters that we would like to measure and analyze on phylogenies, such as morphology, protein sequences, protein structure, gene expression, physiological traits, and environmental tolerances. Different types of character data need to be handled in different ways. In particular, we need to be able to articulate explicit models for how each type of data evolves.
We can group character types based on some shared features. For example, some data are discrete values (such as DNA), others have continuous values (such as mass or length), and still others have countable values (such as number of body segments) that have integer values that come in discrete values like DNA but these integers are ordered and convey magnitude.
Rather than approach each new character type in an ad hoc way, it is important to examine these more general properties and explicitly consider how each character should be encoded and modeled. Specifying the character types is a critical aspect of how we articulate our ontological perspective (i.e., what organismal attributes exist, which are worth considering for the question at hand, and what the relation between them is). The identification of which character type your data correspond to is a decision about measurement theory (Houle et al. 2011) – a field that sits at the intersection of math, statistics, and philosophy that concerns the relationships between measurements and the reality they represent, clarifies what information the measurements contain, examines which mathematical operations we can perform with them, and reveals what actual transforms those operations correspond to. With a name like “measurement theory”, you might assume that it is a dusty and boring annoyance that someone else needs to worry about, but it is actually an exciting and grounding framework for understanding many of the central aspects of what we do in science.
| Scale type | Domain | Measurement type | Permissible transformations | Arbitrary parameters | Meaningful comparisons | Biological examples |
|---|---|---|---|---|---|---|
| Nominal | Any set of symbols | Discrete | Any one-to-one mapping | Countable | Equivalence | Species, genes |
| Ordinal | Ordered symbols | Discrete | Any monotonically increasing function | Countable | Order | Social dominance |
| Interval | Real numbers | Continuous | \(x \rightarrow ax + b\) | 2 | Order, differences | Dates, Malthusian fitness, relative temperature (arbitrary 0, e.g. Celsius and Fahrenheit) |
| Log-interval | Positive real numbers | Continuous | \(x \rightarrow ax^b\) | 2 | Order, ratios | Body size |
| Difference | Real numbers | Continuous | \(x \rightarrow x + a\) | 1 | Order, differences | Log-transformed ratio-scale variables |
| Ratio | Positive real numbers | Continuous | \(x \rightarrow ax\) | 1 | Order, ratios, differences | Length, mass, duration, absolute temperature (e.g. Kelvin) |
| Absolute | Defined | Continuous | None | 0 | Any | Probability |
Since the practice of measurement in evolutionary biology proceeded pragmatically and largely independent of measurement theory, there are some differences in the nomenclature. What phylogenetic biologists call “character type” is referred to in measurement theory, and many other fields of science, as “scale type” (Table 8.1). Scale types vary in several ways. The Domain indicates the possible values. Phylogenetic methods differ most based on whether this domain is discrete or continuous, reflected here in the Scale category column. Permissible transformations indicate the mathematical operations that can be performed without distorting measurement meaning. Arbitrary parameters are the number of values that must be specified to establish a numerical system. For example, for a ratio scale type zero means absence and one arbitrary parameter must be specified, such as an object of standard mass or length. For an interval scale type, zero is arbitrary and two parameters must be specified, such as the temperature at which water freezes and boils. Meaningful comparisons indicates comparisons that can be made between measurements of each scale type.
There are many types of organism measurements, and therefore state spaces and character types, that are addressed in a phylogenetic context. Here we consider some of the more frequently applied character types, i.e. scale types. Different scale types require different models of evolution. The biggest distinction is between discrete character types, like DNA, and continuous character types, like mass, that require radically different models of evolution.
8.1 Discrete character types
8.1.1 Nominal scale types
There are several other frequent applications of nominal scale types beyond DNA sequences in phylogenetic analyses. The most common include others include other molecular sequence data, but they are also used for discrete unordered morphological character states
8.1.1.1 DNA nucleotides
Measurements of DNA sequences have 4 possible states, corresponding to each of the 4 nucleotides – A, C, G, and T. DNA data are discrete and unordered. Nucleotides are discrete because they have a set of distinct and separate states that it can take. They are unordered because changes don’t have to occur in a specific order, any state can change to any other state directly. In measurement theory terms, discrete unordered character types corresponds to a nominal scale type.
8.1.1.2 Amino acids
Protein sequences are handled very similarly to DNA sequences, the character states just correspond to amino acids rather than to DNA nucleotides. They are discrete and unordered, and therefore on a nominal scale type. There are 20 possible states instead of 4, so the primary difference is that the state space is larger. This means there are many more model parameters than for DNA data.
There are a few reasons why protein sequences are often considered rather than the DNA sequences that encode them. One is that questions about protein evolution are best addressed with models that directly describe protein evolution. Another reason is that synonymous changes in protein coding DNA sequences quickly saturate for more distant evolutionary comparisons. This makes it difficult to align sequences, and means that much of the variation in DNA sequence has little information about phylogenetic relationships. Protein data can be more tractable to work with in this situation.
8.1.1.3 Codons
Since there are 4 possible DNA nucleotides and codons are 3 nucleotides long, there are \(4^3=64\) possible codons. Each one of these codons corresponds to a specific amino acid or stop codon. In some cases, it is most interesting to consider each of the 64 codons as a discrete character state. The models then have matrices that have dimensions of 64 (as opposed to 4 for nucleotides and 20 for amino acids).
8.1.1.4 Morphology
Direct analogs of the DNA sequence evolution models are often applied to discrete unordered morphological traits, such as the presence or absence of limbs (Harmon 2018, chap. 7).
8.1.2 Ordinal scale types
Ordinal scale types include measurements such as the number of digits on a forelimb. They differ from nominal scale types in that there is an ordering, i.e. some values are larger than others and there are different distances between the values (Houle et al. 2011, Table 1). Character measurements on an ordinal scale type are often referred to in phylogenetics as discrete ordered character types. An example would be any countable character, such as the number of bristles on an arthropod appendege or the number of digits on a vertebrate forelimb.
Models for the evolution of ordinal data can be described with the same language we used for nominal scale types, the rates for changes between non-adjacent values are just set to zero. 5, for example, will have a nonzero rate of change to 6 and 4 and a rate of zero to all other values. In this way, the rate matrix disallows instantaneous changes that skip intermediate values. For example, to evolve from a forelimb with 5 digits to one with 3 digits, the model requires that the character pass through an intermediate state of 4 digits.
Such a rate matrix that explains the changes between 0-6 digits would have this form, if the rates were the same between all states:
\[\begin{equation} \mathbf{Q} = \left(\begin{array}{ccccccc} -\mu & \mu & 0 & 0 & 0 & 0 & 0 \\ \mu & -2\mu & \mu & 0 & 0 & 0 & 0 \\ 0 & \mu & -2\mu & \mu & 0 & 0 & 0 \\ 0 & 0 & \mu & -2\mu & \mu & 0 & 0 \\ 0 & 0 & 0 & \mu & -2\mu & \mu & 0 \\ 0 & 0 & 0 & 0 & \mu & -2\mu & \mu \\ 0 & 0 & 0 & 0 & 0 & \mu & -\mu \\ \end{array}\right) \end{equation}\]
8.2 Continuous data
Many characters, such as body mass, limb length, protein abundance, maximum swimming speed, and metabolic rate can take on a value within some range of real numbers. These character states are often lumped together by phylogenetic biologists under the single umbrella of continuous character data, since any two values can have values between them. Measurement theory, on the other hand, identifies multiple scale types that all have continuous values.
The evolution of continuous measurements, regardless of specific scale type, are often modeled with the Brownian Motion (BM) family of models. At any point in time, the value can take an incremental step up or down. There are two parameters - the starting value, and the step size per unit time.
The use of BM models for phylogenetic analysis of continuous data is a pragmatic choice, as it greatly simplifies many calculations. But there are many ways in which BM doesn’t actually describe the evolution of continuous traits. For example, BM can result in a value that is any real number, positive or negative, whereas many biological measurements that are considered in a phylogenetic perspective can only take on positive values. Sometimes these discrepancies have little impact, and sometimes they can lead to entirely wrong conclusions.
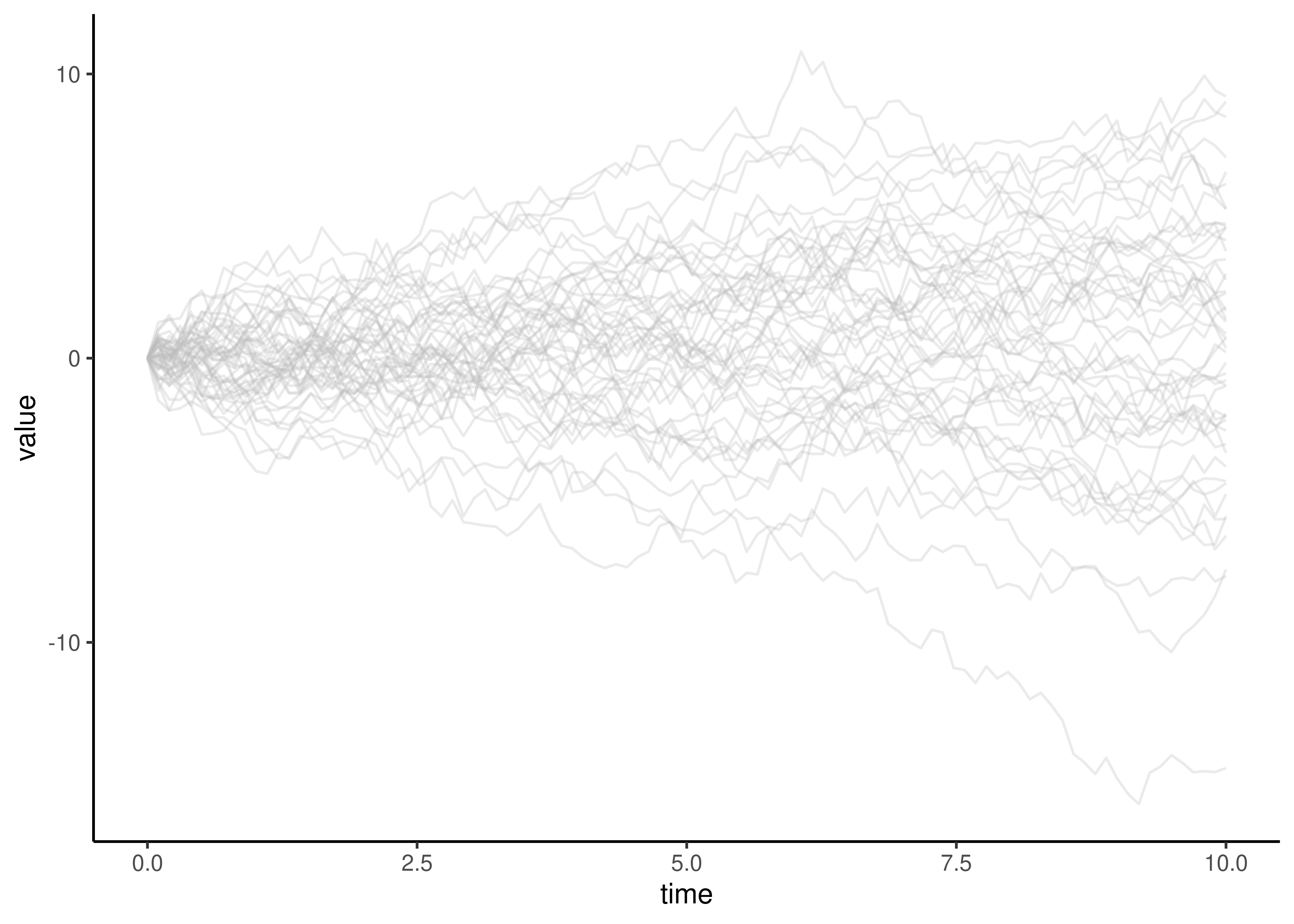
Figure 8.1: Multiple brownian motion trajectories.
8.2.2 Ratio scale type
The most commonly encountered continuous scale type in phylogenetic analyses is the ratio scale type (Houle et al. 2011, Table 1). These measurements can take on values that are positive real numbers. They include many common continuous measurements, such as mass, length, and time interval. The name “ratio scale type” refers to the fact that ratios of these measurements are invariant with respect to units. If the ratio of body lengths of frog A to frog B is 2.38 when measured in centimeters, it will also be 2.38 when measured in inches, miles, or any other unit of length.
Ratio scale type data are often log transformed before phylogenetic analysis. This converts them to difference scale types.