Chapter 9 Phylogenies and time
Phylogenies consider the history, pattern, and process of evolution through time, so time is often a critical feature of phylogenetic analyses. The specific considerations of time vary across analyses and studies, depending on the data available and the questions asked.
It is helpful to step back and think about how the elements of a phylogeny correspond to time. We will here consider rooted trees, where the direction of time is specified and runs from the root to the tips. Each node occurs at a specific point in time, even if the specific time is unknown. We will call this point in time the node age. There is often confusion about the description of relative time on phylogenies. I will describe the magnitude of age here as time before the present. A node minimum age is closer to the present (further forward in time and closer to the tips) and a node with maximum age as further from the present (further back in time). A node is treated as a singular divergence event, and has no duration. This of course is an approximation of the actual biology of divergence, which can take place over a period of time as populations become increasingly isolated.
Each edge (branch) connects two nodes. In a rooted tree, we refer to the node closer to the root (or that is the root) as the parent node, and the node closer to the tips (or that is a tip) as the child node. The starting and ending times of the edge are set by the ages of the parent and child nodes. The duration of the edge is the difference in the ages of these nodes.
9.1 Measurements of time on trees
As discussed in Section 2.5, branch length can mean different things. It is up to the investigator to specify a branch length and clearly communicate what it means in the tree at hand. The three usual approaches are a cladogram (a tree in which branch lengths have no meaning), phylogram (branch lengths are the expected amount of evolutionary change in the traits used to infer the phylogeny), and chronogram, where branch lengths are in units of time. These trees types differ in what we can say about time.
9.1.1 Cladograms
Because branch lengths in a cladogram have no meaning, we cannot make absolute statements about time in a cladogram. This doesn’t mean, though, that we can’t say anything about time – we can still make some ordinal statements about the relative ages of nodes.
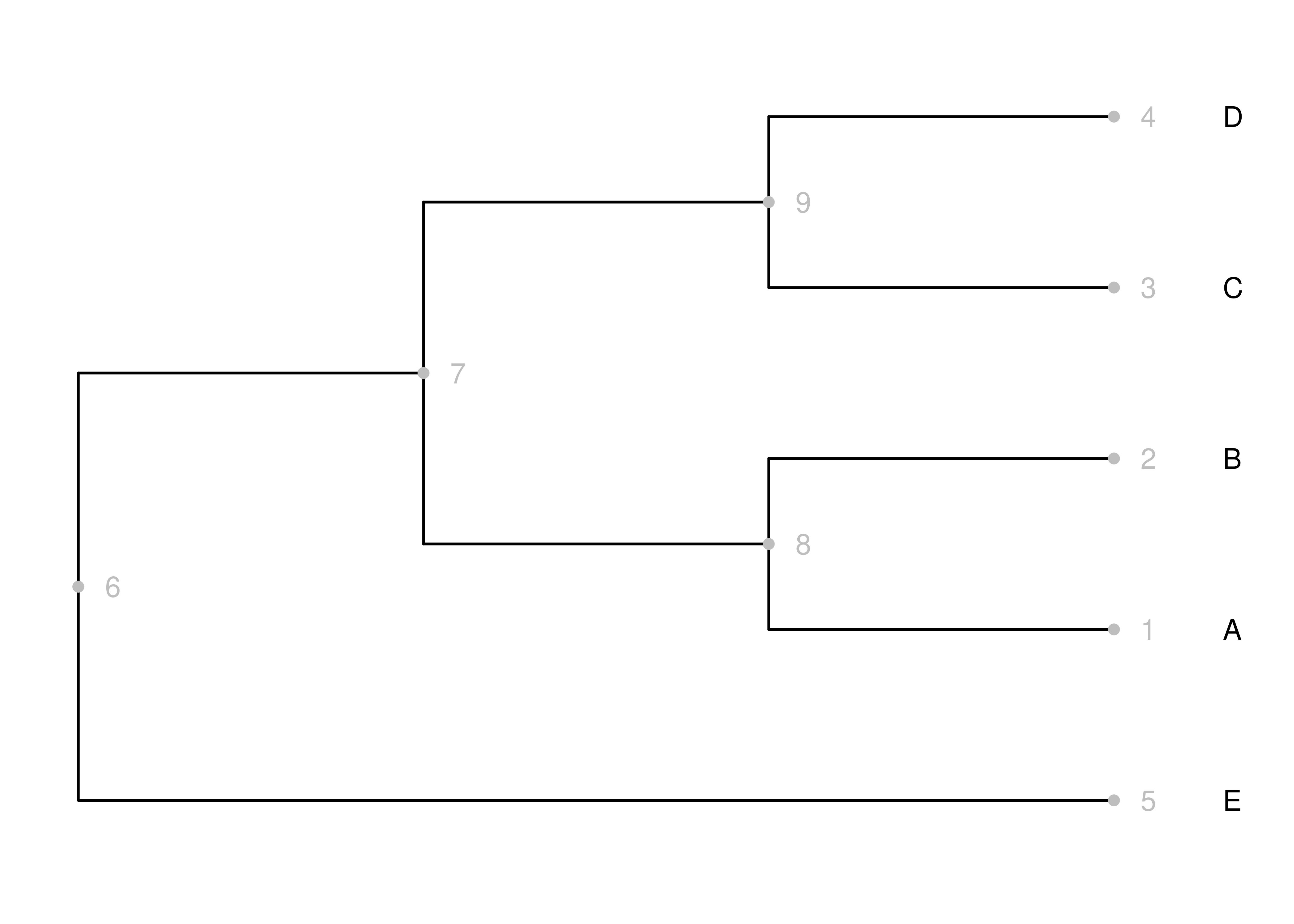
Figure 9.1: A cladogram. Nodes and node numbers are gray, and branches are black.
Take a look at the cladogram in Figure 9.1. Consider the gray node numbers. The terminal nodes are numbered 1-5, and 6-9 are internal nodes. Of those, the root is node 6. Because the tree is rooted, we know that time proceeds from the root to the tips. If you consider two nodes, where one is descended from the other, then the node closer to the root is older. There are a variety of statements we could make based on this simple relationship, including:
- Node 6 is older than all other nodes in the phylogeny. This is tautological, since the root is by definition the oldest node.
- Node 7 is older than node 9. This is because 9 is descended form 7, and 7 is closer to the root.
We can’t make any relative assertions, though, about the ages of nodes that aren’t descended from each other. For example, we have no idea if node 8 or node 9 is older.
In practice, these relative statements of age are often quite useful. For example, if Clade A is nested within Clade B, then we know that Clade A is younger than Clade B even if we don’t know the ages of any nodes. This may seem trivial, but it is important information that is implicit in many discussions of phylogenies.
9.1.2 Phylograms
Strictly speaking, the only assertions we can make about time on phylograms are those that we can also make on cladograms. This is because we can’t be certain of the relationships between time and branch length in the phylogram. If the rate of evolution changes in different regions of the tree, then branches of the same length would not represent time intervals of the same length. Phylograms therefore have the same information about time as cladograms do.
9.1.3 Chronograms
By definition, in a chronogram branch lengths are in units of time. The age of each node is specified. This has a couple implications for what we can say about time. We can make ordinal statements, as we did for cladograms and phylograms. But we can also make absolute statements about the interval of time that has elapsed between two nodes. We can also make statements about the relative ages of nodes that are not descended from each other.
9.2 Time calibration
The process of creating a chronogram is referred to as time calibration. In essence, external information about the ages of some nodes are used to constrain the ages of other nodes.
If the rate of evolution were uniform and did not vary in different lineages, then the branch lengths on the phylogram would be proportional to the elapsed time. We could convert from the phylogram to the chronogram just by dividing branch lengths by the rate of change. For example, if the branch lengths are in number of expected DNA substitutions, and the rate of evolutionary change is always 2 substitutions were million years, then dividing each branch length by 2 would give a chronogram where the units of branch length are millions of years. This is called clock-like evolution – changes in characters are like regular tics on a clock. No real data evolve in a perfectly clock-like way, so time calibration of phylogenies instead relies on relaxed clock models that allow local variations in evolutionary rate.
If all the tip nodes of a phylogeny are the same distance from the root, the tree is referred to as being ultrametric. If all the tips on a chronogram are sampled at the same time, then the chronogram is expected to be ultrametric because the same amount of time has elapsed from the root to each tip. An ultrametric tree is not necessarily a chronogram, though. Some of the internal nodes may have ages that violate branch lengths proportional to time, or a phylogram could be constrained to be ultrametric without calibrating any of the branch lengths according to time.
In the early days of the field, phylogenetic inference was done separately from time calibration. A phylogram would first be inferred. The phylogram would then be modified into a chronogram. This would involve stretching and shrinking branches to make the tree ultrametric and to constrain some internal nodes to fit fossil calibration dates. This modification of branch lengths was not made with consideration of the underlying trait data.
Subsequent approaches instead unify phylogenetic inference and time calibration. Using external information, such as fossils and the sampling times of tips, branch lengths are inferred in units of time under relaxed clock models that allow rates of evolution to vary across the tree to accommodate these constraints. Because the external calibrations allow rates and time to be inferred independently (unlike an unconstrained phylogram, where they are conflated), this time calibrated inference produces a chronogram.
9.3 The implications of constraining node ages
Clamping the ages of nodes reduces the number of free parameters in our tree. The way to think about this is that the more information we have, the more constrained and specific our view of the world is. Consider first constraining tip ages to make a tree ultrametric. Before we clamp the tip ages, any tip can be any age and all the branches are free to have any length. The ultrametric tree is nested within this set of unconstrained possibilities. The tip ages, and therefore branch lengths, in this unconstrained tree can be selected so that they are ultrametric, but the vast majority of values will lead to trees that are not ultrametric. By clamping some values with added information that some nodes (tips, in this case) are the same age, we now are allowing only a constrained subset of trees and these require fewer parameters to describe.
Consider this same task in terms of branch lengths, rather than node ages. From Section 2.3, we know that the number of branches in a tree is \(2n-2\), where \(n\) is the number of tips. This is because each of the \(n\) tip nodes has an branch leading to it, and each of the \(n-1\) internal nodes, with the exception of the root node, has an branch leading to it. So there are \(n-2\) branches that give rise to internal nodes. This is how we arrive at our \(n+n-2=2n-2\) branches in the phylogeny, each with their own length. In an ultrametric tree, by definition all the tips have the same age. That means that if you know the length of one of the branches leading to a tip node, you can calculate all the others. They have a deterministic relationship and are not free to vary independently. Rather than \(n\) branch lengths for the tips, we only have \(1\) tip branch length that is free to vary and we can calculate all the others so that the tip nodes have the same ages. This leaves us with \(1+n-2=n-1\) branch lengths that we need to estimate independently in our ultrametric tree.
9.3.1 Time calibration in practice
The use of character data and time calibrations to infer time calibrated phylogenies fall into two broad categories. The first is to use information from fossils (or other historical data) to constrain the ages of internal nodes. A Bayesian framework provides a natural framework for this – node ages can by specified as priors on the tree. For example, if a given fossil is known to fall within a particular clade, then the most recent common ancestor of that clade can be constrained to be at least as old as the fossil and possibly older.
While this can work well in some situations, there are several drawbacks to this method. In practice, it is also necessary to place maximum ages on some of the nodes to keep the time calibration from pushing everything way back in time. Given the incompleteness of the fossil record, this is not as straight forward as constraining the minimum age of a node. If we have a fossil we can assert that the clade that contains it can be no younger than that specimen, though it may be much older. But it is harder to assert a maximum age, given that we just might not have fossils for older organisms that existed in the clade. Applying maximum ages often relies on expertise and additional information, such as knowledge that a given land mass where the organisms are exclusively found did not exist before a particular time.
Models known as the “fossilized birth–death” (FBD) process don’t use fossils as external constraints on internal nodes, they instead include fossils right in the tree as their own tips (Heath et al. 2014). Unlike extant tips, which all have the same age (i.e., today), the ages of these fossil tips are then constrained with geological data. This approach provides the ability to also include parameters for fossil preservation and sampling. FBD methods require that the character matrix includes data that can be scored in the fossils.